Unidad 3 para primero de Bachillerato

TEMA 3. LÓGICA DE ENUNCIADOS

Este tema pretende dar a conocer de un modo elemental los principios básicos de la lógica de enunciados.

La lógica de enunciados o de proposiciones es el nivel más básico de análisis lógico. Se analizan las relaciones que se dan entre los enunciados o las proposiciones; es, pues, una lógica interproposicional, no intraproposicional. En este nivel se simboliza de la misma manera proposiciones o enunciados de contenido tan diferente como: "ahora llueve", "algunos días llueve" o "todos los días llueve".

¿Qué es uno enunciando o una proposición? Una oración declarativa que puede ser verdadera o falsa. Los enunciados dicen de las cosas y, consecuentemente, pueden ser verdaderos o falsos. No son enunciados las expresiones lingüísticas interrogativas, exclamativas o imperativas.

Los enunciados o proposiciones pueden ser atómicos o simples, los que no se pueden descomponer en otros; y moleculares o complejos, los que sí se pueden descomponer.

1. Lenguaje natural y lenguaje formalizado. Noción de enunciado.
Entendemos por lenguaje natural o cotidiano las lenguas maternas (francés, español etc.), y entenderemos por lenguaje formalizado el lenguaje simbólico propio de la lógica de enunciados.
Un enunciado es un conjunto de palabras que pretende indicar, de un modo claro y preciso, un comportamiento o modo de ser de la realidad. La propiedad esencial de los enunciados es la posibilidad que tienen de ser verdaderos o falsos. Así, diremos que un enunciado tiene el valor de verdad V cuando lo que dice se corresponde con lo que ocurre en la realidad; y tendrá el valor de verdad F cuando lo que dice no se corresponde con lo que ocurre en la realidad. Por ejemplo, el enunciado "Francia es un país europeo" tendrá la propiedad V.
Por otro lado, como ya hemos dicho anteriormente, los enunciados pueden ser simples o complejos. Un enunciado simple es aquel que no contiene otros enunciados como partes suyas (por ejemplo "María es rubia"). Un enunciado complejo es aquel que contiene otros enunciados con partes suya (por ejemplo, "María es rubia y Pedro es moreno").
2. El lenguaje formalizado de la lógica.
El lenguaje formalizado de la lógica sirve para reconstruir la estructura del lenguaje natural en lo que respecta al modo en cómo están conectados los enunciados simples conformando enunciados complejos. El lenguaje formalizado de la lógica constará básicamente de dos tipos de signos:
1) Letras enunciativas o variables proposicionales: signos para representar a los enunciados simples.
2) Conectivas o funtores enunciativos: signos para representar las conexiones entre enunciados simples.
 
Además, habría que incluir un tercer elemento en este lenguaje que son los paréntesis que se usarán para la correcta escritura de las fórmulas lógicas.

2.1.Letras enunciativas o variables proposicionales
En el lenguaje formalizado de la lógica, los enunciados se simbolizan por las letras "p", "q", "r", "s", "t" hasta la "z", las cuales se denominan letras enunciativas o variables proposicionales. Por ejemplo, dados los enunciados "el peso es una propiedad física" y "las focas se alimentan de peces", podemos representarlos en el lenguaje formal por "q" y por "p" respectivamente.
"el peso es una propiedad física"= q
"las focas se alimentan de peces"= p

2.2. Funtores enunciativos o conectivas.

Son signos para representar las conexiones entre enunciados. Son cinco:

 

Negador: ¬ Se lee "No"

Conjuntor: Λ Se lee "y"

Disyuntor inclusivo: V Se lee "o"

Disyuntor exclusivo: ›─‹ Se lee “o”

Implicador: → Se lee "implica" o "si...entonces..."

Equivaledor: ↔ Se lee "equivale" o "si y sólo si...entonces..."

2.2.1. Negador.

En el lenguaje natural, por motivos estilísticos, oratorios o literarios, usamos indistintamente diversas expresiones para negar una oración o varias oraciones (por ejemplo, "no es cierto que..."; "no es el caso que...", "no ocurre que" o sencillamente "no"). Pues bien, todas las oraciones que se enuncian con estas u otras expresiones en el lenguaje simbólico de la lógica se formulan con el signo lógico negador delante de la oración (u oraciones) a la que afectan. Por ejemplo:

"No es cierto que Juan viniera" = "¬p"

(siendo "p" = "Juan vino")

En el supuesto de que la oración estuviese negada en el lenguaje natural por dos veces, habría que escribir dos signos lógicos negadores (doble negador) delante de la letra enunciativa en cuestión. Por ejemplo:

"No es cierto que Juan no viniera" = "¬¬p"

(siendo "p" = "Juan vino")

Por otra parte, estableceremos para cada conectiva lógica una regla semántica y una tabla de verdad. En el caso del negador, como es obvio, la regla dice que si un enunciado es verdadero, entonces su negación es falsa; y si un enunciado es falso, su negación es verdadera. La tabla de verdad es:

 

p	¬p	¬¬p
V	F	V
F	V	F

 

 

2.2.2.Conjuntor
El signo lógico conjuntor enlaza o vincula a dos enunciados (o más) estableciendo enunciados complejos. Las fórmulas lógicas generadas por el uso de un conjuntor en una fórmula se denominan conjunciones. Por ejemplo: "p Λ q" es una conjunción.
En el lenguaje natural el signo lógico conjuntor simboliza expresiones como: "y", "pero", "no obstante", "sin embargo" etc. Por ejemplo, el enunciado complejo:
" Llueve pero hace calor" = " p Λ q"
(siendo "p"= " Llueve" ; "q"="Hace calor")
La regla del conjuntor nos dice que una conjunción sólo será verdadera cuando sus miembros son todos verdaderos. Es obvio que las combinaciones de valores veritativos serán: ambos verdaderos; el primero verdadero y el segundo falso, el primero falso y el segundo verdadero; y ambos falsos. La tabla de verdad de la conjunción es:
 

2.2.3. Disyuntor inclusivo.
Las fórmulas lógicas originadas por el uso del disyuntor se denominan disyunciones. Por ejemplo, "pVq" es una disyunción. En el lenguaje natural el disyuntor simboliza expresiones como "o", "o bien...o bien...", etc.
Por ejemplo, el enunciado complejo:
" Llueve o nieva" = "pVq"
(siendo "p"="Llueve" y "q"="Nieva")
La regla del disyuntor nos dice que una disyunción sólo será falsa cuando ambos miembros sean falsos. La tabla de verdad de la disyunción será:

2.2.4.Disyuntor exclusivo
La disyunción exclusiva obliga a que sólo una de las opciones sea verdadera pero no las dos al mismo tiempo por crear una contradicción. Es decir, que solo será verdadera cuando sus dos miembros son de distinto valor.

p	q	p›─‹q
V	V	F
V	F	V
F	V	V
F	F	F

2.2.5.Implicador o condicional
Las fórmulas lógicas generadas por el uso del implicador se deniminan implicaciones. Por ejemplo, "p→q" es una implicación. Las expresiones del lenguaje natural que son simbolizadas por el implicador son; "si...entonces"; "implica" etc. Por ejemplo, el enunciado complejo:
" Si llueve entonces nos quedamos en casa"= "p→q"
(siendo "p"="Llueve" y "q"="nos quedaremos en casa")
La regla de la implicación dice que una implicación sólo será falsa cuando su primer miembro sea verdadero y su segundo miembro falso. La tabla es:
   
2.2.6.Equivaledor o bicondicional
Las fórmulas lógicas originadas por el uso del equivaledor se denominan equivalencias. Por ejemplo, "p↔q" es una equivalencia. Las expresiones del lenguaje natural que se simbolizan mediante el equivaledor son: "si y sólo sí...entonces..."; "equivale" etc. Por ejemplo, el enunciado complejo:
" Si y sólo si hoy es Lunes entonces mañana es Martes" =" p↔q"
("siendo p"="Hoy es Lunes" y "q"="mañana es Martes")
La regla de la equivalencia dice que una equivalencia sólo será verdadera si sus miembros son del mismo valor veritativos. Por tanto, la tabla será:
 

2.3.Reglas de formación de fórmulas lógicas
1ª regla: "p”, "q", "r" etc. son fórmulas lógicas.
 
2ª regla: "p Λ q"(conjunción); "p V q"(disyunción); "p → q" (implicación); "p ↔ q" (equivalencia) son fórmulas lógicas.
 
3ª regla: en el caso de que en la fórmula haya más de una conectiva, la capacidad para ser conectiva principal viene dada por el siguiente orden:
Equivaledor: ↔                                 +
Implicador: →
Disyuntor exclusivo: ›─‹
Disyuntor inclusivo: V
Conjuntor: Λ                                        -
            Ejemplos:
                La fórmula "p Λ q → p" será una implicación cuyo primer miembro es una conjunción (“p Λ q”) y cuyo segundo miembro una letra enunciativa ("p").
                La fórmula "p V q ↔ q Λ p" será una equivalencia cuyo primer miembro es una disyunción (“p V q”) y cuyo segundo miembro es una conjunción ("q Λ p").
                La fórmula "r V z Λ t" será una disyunción cuyo primer miembro es una letra enunciativa ("r") y cuyo segundo miembro es una conjunción ("z Λ t").
 
4ª regla: los paréntesis indican que las subfórmulas que van encerradas en ellos son parte de otra fórmula principal.
                Ejemplos:
                        "(p ↔ x) V (p → x)" será una disyunción cuyo primer miembro es una equivalencia("p ↔ x") y cuyo segundo miembro es una implicación("p → x")
                        "r Λ (t V s)" será una conjunción cuyo primer miembro es una letra enunciativa ("r") y cuyo segundo miembro es una disyunción("t V s")
 
5ª regla: el negador afecta a aquella letra enunciativa o subfórmula que está a su derecha.
                    Ejemplos:
                        "¬p" es la negación de "p". Se lee "no p"
                        “¬ (r → q)" es la negación de una implicación.
                        "¬ (x V s) Λ ¬ (p → q)" es una conjunción que tiene como primer miembro la negación de una disyunción y como segundo miembro la negación de una implicación.
Actividad 1:
Ahora intenta simbolizar estas frases:

1.- Puedo estudiar ciencias o humanidades. Y si estudio ciencias, entonces podré hacer Medicina. Y si estudio humanidades, podré hacer Magisterio. Y no quiero hacer Magisterio. Por tanto, estudiaré ciencias.

2.- Ni te esfuerzas por aprender ni quieres trabajar. Y si no te esfuerzas por aprender, entonces no podrás sacar unos estudios. Y si no trabajas, entonces no podrás ganarte la vida. Por tanto, o trabajas o te esfuerzas por aprender.

3.- Si voy a verte, entonces te llevaré un bizcocho. Y no te he llevado bizcocho. Luego no he ido a verte.

4.- No es posible que ni me hayas visto ni me hayas oido. Y tú dices que no me has oido. Por tanto, me has visto.

5.- Hace frío. Y si hace frío, entonces pondré el edredón. Y si pongo el edredón, entonces guardaré la colcha. Por consiguiente, guardaré la colcha.

Actividad 2: Realiza los siguientes ejercicios 

EJERCICIOS DE SIMBOLIZACIÓN EN LÓGICA PROPOSICIONAL

1.- [(((pVq) ^(pàr)) ^(qàs)) ^ ¬s] àp

2.- [((¬p^¬q) ^(¬pà¬r))^(¬qà¬s)]à(qVp)

3.- [(pàq) ^¬q]à¬p

4.- [¬(¬p^¬q) ^¬q]àp

5.- [(p ^(pàq) ^(qàr)]àr

  REGLAS DE INFERENCIA

1. Adición (LA):

Forma esquemática

p

pÚq

2. simplificación (S):

Forma esquemática

pÙq

p

3.Union

Forma esquemática

p

q

pÙq

4. Modus ponendo ponens (MP):

Forma esquemática

p®q

p

q

5. Modus tollendo tollens (MT):

Forma esquemática

p®q

∼q ∼p

Leyes

p®(pÚq)

(pÙq)®p                                           

(pÙq) ® (pÙq)

(p®q)Ùp®q

 ( p ® q ) Ù ∼q  ® ∼p

6. Modus tollendo ponens o silogismo disyuntivo

Forma esquemática

pÚq

∼p

q

7. Negación de la implicación

        

               ∼ (p®q)

                 ____________

                 pÙ∼ q

8. Definición de la equivalencia

               p↔q

                  ____________

                      ( p ® q ) Ù  ( p ®q)

                  

               

 ( p Ú q ) Ù ∼p  ® q

∼ (p®q) ↔ pÙ∼ q

(p↔q) ↔( p ® q ) Ù ( p ®q)

Importante: Se comprueba la validez de estas reglas de inferencia, demostrando que la correspondiente condicionalasociada es una tautología. 

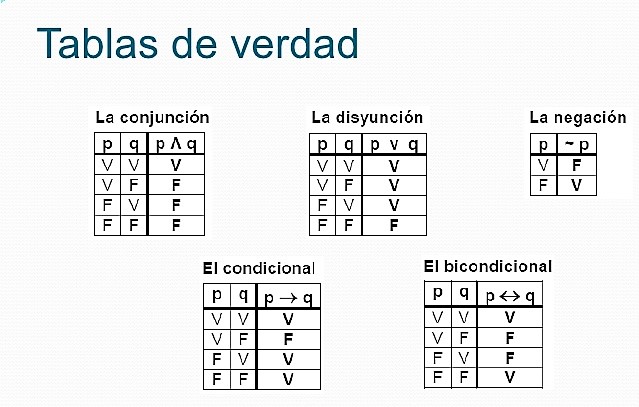
Ejemplo de tabla de verdad

 

                                      Ejercicios de Lógica: 

• Apuntes de Lógica proposicional
• Ejercicios de tablas de verdad
• Ejercicios de cálculo (nivel principiante)
• Ejercicios de cálculo reueltos (nivel principiante)
• Ejercicios de cálculo (nivel medio)
• Ejercicios de formalización
• Ejercicios de formalización resueltos
• Problemas de Lógica
• Falacias